[4편] 프리즘으로 생존 분석 그래프(survival curve analysis) 만들기

 

 

생존곡선(survival curve)이란?

생존곡선은 말 그대로, 시간이 지남에 따라 대상(사람, 동물, 세포 등)이 얼마나 살아남았는지를 보여주는 그래프입니다.
단순히 누가 살았고 죽었는지를 넘어서, ‘언제’ 이벤트가 발생했는지를 반영하기 때문에, 치료제의 효과나 질병의 경과를 분석할 때 매우 유용합니다. 즉 생존률 차이를 시각화하는 가장 명확한 방법입니다.

---

 

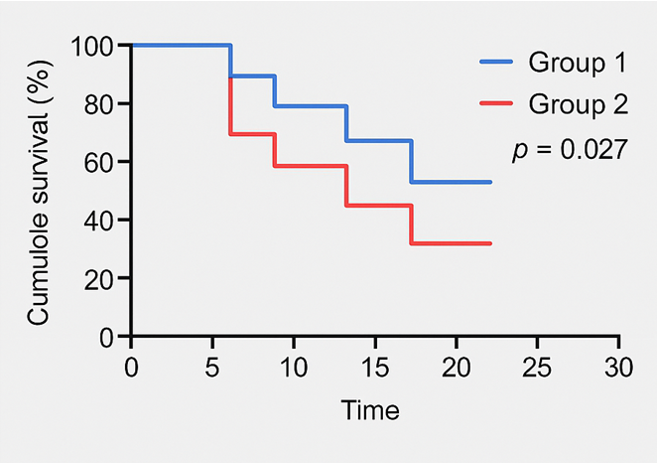
왜 Kaplan-Meier 그래프가 중요한가요?

생존률을 ‘평균 생존일수’ 같은 하나의 숫자로 요약하는 것은 실제 차이를 놓치게 만들 수 있습니다.
Kaplan-Meier 그래프는 시간 전체를 반영한 생존의 ‘모양’과 흐름을 보여줌으로써, 특정 시점에서 위험이 급격히 증가하거나 회복이 일어나는 패턴을 시각적으로 드러냅니다.

---

그래프 의미

환자(또는 실험군)의 생존률(%)이 시간에 따라 감소하는 곡선
각 그룹의 생존 차이를 Log-rank test로 통계 처리
Censoring 정보(중도탈락 등) 시각화 가능

 

---

그래프 생성 절차 (프리즘 프로토콜 STEP 1 ~5)

STEP 1. 설정

 

New Table & Graph → Survival 선택

선택: “Survival table” → “Enter time-to-event data”

 

STEP 2. 데이터 입력

각 그룹별로 생존 시간(time)과 status (1=event, 0=censored) 입력

 

STEP 3. 그래프 생성

Kaplan-Meier 곡선 자동 생성

Censoring (X 마크) 표시 옵션 켜기

 

STEP 4. Log-rank test 실행

Analyze → Compare survival curves → Log-rank (Mantel-Cox test)

p-value, hazard ratio 제공

 

STEP 5. 그래프에 결과 삽입

Graph → “Add Results to Graph” → p-value 또는 해석 텍스트 삽입

 

---

Kaplan-Meier 곡선은 언제 쓰나요?

Kaplan-Meier 생존곡선은 다음과 같은 상황에서 사용됩니다:

신약이 생존 기간을 연장하는지를 알고 싶을 때

두 치료군 간에 사망률 차이가 있는지를 분석할 때

동물실험에서 생존률 비교가 필요한 경우

이 곡선은 각 시간 지점에서의 생존 확률을 계산하고, 계단식 형태로 그래프가 그려집니다.
특히 Censoring(중도탈락) 처리를 통해, 아직 사망하지 않았지만 관찰이 종료된 대상도 반영할 수 있습니다.

 

---

Log-rank test는 왜 필요한가요?

그래프만 보면 차이가 있어 보이더라도, 통계적으로 유의미한 차이인지는 알 수 없습니다.
그래서 Kaplan-Meier 곡선은 보통 Log-rank test와 함께 사용됩니다.

Log-rank test는 두 곡선 사이의 전반적인 차이를 검정하며, 일반적인 기준은 아래와 같습니다:

P-value 해석
< 0.05: 생존곡선 간 유의미한 차이 있음
≥ 0.05: 차이가 통계적으로 유의하지 않음

Prism에서는 Log-rank (Mantel-Cox) test를 매우 쉽게 수행할 수 있으며, Hazard ratio 같은 추가 정보도 함께 제공됩니다.